Доповідач
Опис
In the present work, we study nonlinear dynamics of the wave triplet with frequencies $\omega_n\approx-n\omega_{ci}$, $n = (-1, 0, 1)$, where $\omega_{ci}$ is the ion cyclotron frequency. The analysis is carried out in the framework of simplified version of the so called ‘cyclokinetics’ described in [1]. Growth rate of the $n = 0$ drift wave, $\gamma_0>0$, and damping rates of the $n=\pm1$ cyclotron waves, $\gamma_{\pm1}<0$, are considered as free parameters. The system of coupled nonlinear equations for the amplitudes of the triplet companions and their phase mismatch has a fixed point solution (Fig.1), i.e. the power is transferred from the unstable drift wave to the damped cyclotron companions.
Under physically relevant condition $|\gamma_1|\gg|\gamma_{-1}|$ [2], fixed-point solution shown in Fig.1 becomes unstable. Shown by the bold line in Fig.2 is the boundary between stable fixed points and stable limit cycles on the $(\Delta,\nu_2)$ plane, for $\nu_3=|\gamma_{-1}|/\gamma_0=2$.
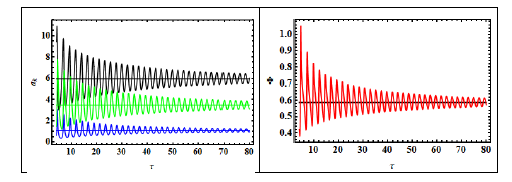
Fig.1. An example of the fixed-point solution for the normalized parameters $\Delta=\delta/\gamma_0=8.66$, with $\delta$ the frequency mismatch, $\nu_3=|\gamma_{-1}|/\gamma_0=2$, $\nu_2=|\gamma_1|/\gamma_0=12$. Shown in the left plot are amplitudes $a_n$ with $n = 0$ (black), $n = -1$ (green), and $n = 1$ (blue). The right plot is the phase mismatch $\Phi,\tau=\gamma_0t$.

Fig.2. Critical curve $\Delta_{cr}(\nu_2,\nu_3=2)$ (bold line). Fixed points are stable for $\Delta>\Delta_{cr}$. Dashed line is $\Delta=\delta/\gamma_0=8.66$. Hopf bifurcation occurs at $\nu_{2\,cr}=12.6$.
An example of the stable limit cycle is shown in Fig.3 for $\nu_2=20$. Cyclotron companions exhibit well separated pulses of their amplitudes, which are accompanied by sudden jumps of the phase mismatch, the latter is mainly responsible for the high incoherency of the signals on the synthetic spectrograms shown in Fig.4. Note that the peak power of the signal with $\omega\approx-\omega_{ci}$ is an order of magnitude lower than that with $\omega\approx\omega_{ci}$, as shown in Fig.5.
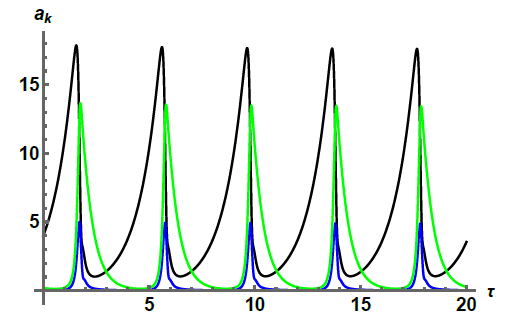
Fig.3. An example of the stable limit cycle for $\Delta=\delta/\gamma_0=8.66$, $\nu_3=|\gamma_{-1}|/\gamma_0=2$, $\nu_2=|\gamma_1|/\gamma_0=20$. The color code is the same as in the left plot of Fig.1.
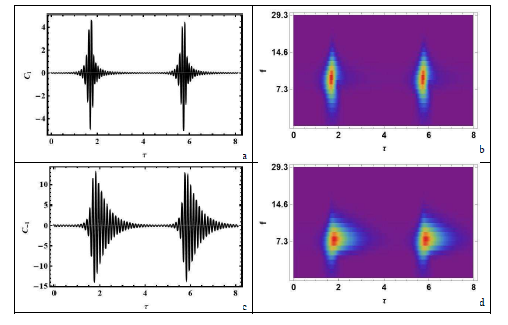
Fig.4. Real parts of the normalized potentials $C_n=\mathrm{Re}\phi_n(\tau)$ with $n=\pm1$ (a,c) and corresponding scalograms of the full signals $\phi_n$ (b,d), for the limit cycle shown in Fig.3. Here and in Fig.5, $f=|\omega_n|/2\pi$.
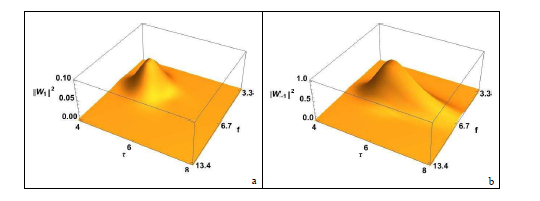
Fig.5. Power spectrum $|\tilde n_e(f,\tau)|^2$ (normalized to 1 for $n=-1$) for the separate burst shown in Fig.3. Note that $|W_1/W_{-1}|^2 \approx\gamma_{-1}/\gamma_1=0.1$.
In summary, the low-frequency unstable drift wave can excite the pair of high-frequency damped ion cyclotron waves with $\omega\approx\pm\omega_{ci}$. Due to huge damping of the companion with $\omega\approx-\omega_{ci}$, nonlinear dynamics of the triplet exhibit stable limit cycles with well separated bursts of the amplitudes, accompanied by the sudden jumps of the phase mismatch between companions. All these features are broadly consistent with observations of the ‘ion cyclotron emission’ in the Ohmic shots at the MAST-U spherical torus [3].
- R.E. Waltz and Z. Deng, Phys. Plasmas 20, 012507 (2016).
- M. Raeth and K. Hallatschek, arXiv:2310.1598v1, 24 Oct 2023.
- N.A. Crocker et al. «New experimental measurements of the core ion cyclotron emission via Doppler back-scattering in MAST-U Ohmic plasmas», 30th ITPA Topical Group meeting on Energetic Particle Physics, Culham Centre for Fusion energy, Abigdon UK, 23-24 October 2023.

