Доповідач
Опис
Розглянуто особливості динаміки резонансної взаємодії трьох хвиль, одна з яких лінійно нестійка, а дві інші хвилі лінійно стійкі. В наближенні слабкої взаємодії хвиль система диференціальних рівнянь для комплексних амплітуд $С$ має вигляд [1-8]
$\quad\quad\frac{dC_1}{dt}=\gamma_1C_1+M_1C_2C_3e^{-i\delta t},$
$\quad\quad\frac{dC_2}{dt}=-\gamma_2C_2-M_2C_1C_3^*e^{i\delta t},$
$\quad\quad\frac{dC_3}{dt}=-\gamma_3C_3-M_3C_1C_2^*e^{i\delta t},(1)$
де $t$ - час, $i$ - уявна одиниця, коефіцієнти $\gamma_k$, $M_k$, $k=1,2,3$ додатні, $\delta=\omega_1-\omega_2-\omega_3\ne0$ - розлад частот хвиль, $C_k^*$ - величини, комплексно спряжені до $C_k$. Шляхом лінійних перетворень [2-5] рівняння (1) зводяться до чотирьох автономних диференціальних рівнянь з дійсними коефіцієнтами для амплітуд хвиль $a_1,a_2,a_3$ та узагальненої фази $\Phi=\Phi_1-\Phi_2-\Phi_3$ [1-3, 6]
$\quad\quad\frac{da_1}{d\tau}=a_1+a_2a_3\cos\Phi, \frac{da_2}{d\tau}=-\nu_2a_2-a_1a_3\cos\Phi,$
$\quad\quad\frac{da_3}{d\tau}=-\nu_3a_3-a_1a_2\cos\Phi, \frac{d\Phi}{d\tau}=\Delta+\left(\frac{a_2a_3}{a_1}-\frac{a_1a_3}{a_2}-\frac{a_1a_2}{a_3}\right)\sin\Phi,(2)$
де введено наступні безрозмірні змінні $\tau=\gamma_1t$,$\nu_2=\gamma_2/\gamma_1$, $\nu_3=\gamma_3/\gamma_1$, $\Delta=\delta/\gamma_1$.
Якщо ж загасання симетричне, $\nu_2=\nu_3$, і початкові умови для $a_2$ та $a_3$ однакові, то поклавши $a_2(t)=a_3(t)$, систему (2) можна замінити на більш просту трьох автономних диференціальних рівнянь
$\quad\quad\frac{da_1}{d\tau}=a_1+a_2^2\cos\Phi,$
$\quad\quad\frac{da_2}{d\tau}=-\nu_2a_2-a_1a_2\cos\Phi, \frac{d\Phi}{d\tau}=\Delta+\left(\frac{a_2^2}{a_1}-2a_1\right)\sin\Phi, (3)$
з двома параметрами $\nu_2$ та $\Delta$.
Властивості поведінки розв’язків рівнянь (3) детально вивчалися в роботах [1-8]. Як показано в [1, 2], якщо $\Delta<\Delta_{min}=3.73$, то в діапазоні $0<\nu_2<\nu_{cr}(\Delta)$ амплітуди хвиль експоненційно зростають. Функція $\nu_{cr}(\Delta)$ монотонно зростає при зменшенні $\Delta$ [4]: $\nu_{cr}(\Delta_{min})\approx2.2$, $\nu_{cr}(2)\approx3$, $\nu_{cr}(1)\approx3.7$, $\nu_{cr}(0.5)\approx4.4$. При $\nu_2\geq\nu_{cr}(\Delta)$ спочатку виникають граничні цикли, далі існують квазіперіодичні та хаотичні траєкторії. Біфуркаційні діаграми для максимальних значень амплітуди $a_3(t)$ у випадку симетричного загасання при різних $\Delta$ показано на рис. 1. Розрахунки біфуркаційних діаграм виконані в пакеті Mathematica 11 [9] за допомогою програми, наведеної в роботі [10].
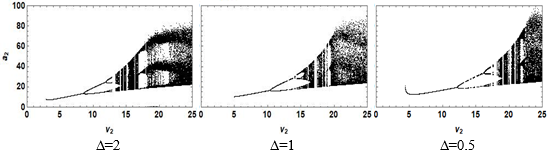
Рис. 1. Біфуркаційні діаграми $\mathrm{max}a_3(\nu_2)$ для випадку симетричного загасання хвиль, $\nu_3=\nu_2$, при різних значеннях розладу частот $\Delta$.
Зовсім інший якісний характер біфуркаційних діаграм буде в випадку несиметричного загасання хвиль $\nu_3\ne\nu_2$ , якщо одне з загасань невелике. На рис. 2 наведені біфуркаційні діаграми для максимальних значень $\max a_3(\nu_2)$ при фіксованому $\nu_3=3$ для різних $\nu_2$ для тих самих значень $\Delta$ , що й на рис. 1.
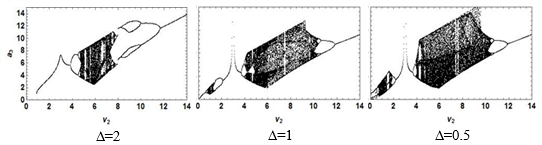
Рис. 2. Біфуркаційні діаграми $\mathrm{max}a_3(\nu_2)$ для $\nu_3=3$ при різних значеннях розладу частот $\Delta$.
З рис. 2 видно, що якщо $\Delta=2$ , то при $0<\nu_2<0.895$ матимемо стійкі стаціонарні розв’язки $a_{3s}\sim\sqrt\nu_2$ . В діапазоні $0.895<\nu_2<3.84$ реалізуються граничні цикли. Квазіперіодичні та хаотичні траєкторії спостерігаються при $4.9<\nu_2<7$, а при $8<\nu_2<12$ виникають зворотні біфуркації граничних циклів $4\rightarrow2\rightarrow1$.
Якщо $\Delta=1$, то при $0<\nu_2<0.19$ матимемо стійкі стаціонарні розв’язки $a_{3s}\sim\sqrt\nu_2$ , а в діапазоні $0.19<\nu_2<0.8$ - граничні цикли. Квазіперіодичні та хаотичні траєкторії спостерігаються при $0.8<\nu_2<1.25$, а при $1.25<\nu_2<2.03$ - зворотні біфуркації. При $2.03<\nu_2<3$ існує граничний цикл, амплітуда якого прямує до нескінченності, якщо $\nu_2\rightarrow3_{-0}$. При $3_{+0}<\nu_2<3.7$ існує граничний цикл, амплітуда якого при збільшенні $\nu_2$ зменшується. В діапазоні $3.7<\nu_2<4.1$ мають місце біфуркації подвоєння періоду, а при $4.1<\nu_2<8$ спостерігаються квазіперіодичні та хаотичні траєкторії. При $10<\nu_2<14$ спостерігаються зворотні біфуркації граничних циклів.
Приблизно така сама якісна картина буде і в випадку $\Delta=0.5$, тільки не існує стійких стаціонарних розв’язків системи (2).
Отже, при несиметричному загасанні хвиль з достатньо невеликими декрементами $\gamma_2,\gamma_3$, якщо $\gamma_1<\gamma_2+\gamma_3$, $\max(\gamma_2,\gamma_3)<4\gamma_1$ і $\delta\leq2\gamma_1$ , то існують розв’язки системи (2) у вигляді граничних циклів, квазіперіодичних та хаотичних траєкторій. Навпаки, в симетричному випадку $\gamma_2=\gamma_3$ або близькому до нього, $\gamma_2\approx\gamma_3$ і $\delta\leq2\gamma_1$ при невеликих $\gamma_2,\gamma_3$ обмежених розв’язків системи (3) взагалі не існує.
- S.Ya. Vyshkind and M.I. Rabinovich, Sov. Phys.-JETP 44 (1976) 292.
- S.Ya. Vyshkind. Radiophysics and Quantum Electronics, 21 (1978) 600.
- J.M. Wersinger, J. M. Finn, and E. Ott, Phys. Fluids 23 (1980) 1142.
- M. N. Bussac, Phys. Scripta, T2/1 (1982) 110.
- C. Meunier, M.N. Bussac, G. Laval, Physica D 4(2) (1982) 236.
- P. Terry and W. Horton, Phys. Fluids 25(1982) 491.
- A. C.‑L. Chian, F. A. Borotto, T. Hada et al., Rev. Mod. Plasma Phys. 6 (2022) 34.
- V. S. Marchenko, S. N. Reznik, Ya. I. Kolesnichenko, Phys. Plasmas 31 (2024) 022507.
- https://reference.wolfram.com/language/tutorial/NDSolveOverview.html.
- J. M. Ginoux,, B. Rosetto. Chaotic Dynamical Systems Tools. Bifurcation diagrams with Mathematica http://ginoux.univ-tln.fr/Recherche/International%20Mathematica%20Symposium.pdf.

